All players regardless of what they say they want from the game, really hope to win big. As you know, there is no method to completely eliminate the casinos edge; even blackjack basic strategy cannot do that. Therefore, players who wanted to win more decided they needed a stronger tool against casinos. Card counting is the only legal method to reduce the house edge and to feel more confident in the casino.

Blackjack Card Counting

We generally classify counting systems on ‘levels’. The Hi/Lo is a ‘one-level’ system, because all the point values are +1, 0 or -1. A ‘two-level’ system uses +2, +1, 0 -1, -2 and a three-level system counts one or more cards as 3, etc. You get the idea. The most common variations of card counting in blackjack are based on statistical evidence that high cards (especially aces and 10s, and to a lesser extent 9s) benefit the player more than the dealer, while the low cards, (3s, 4s, 6s, and especially 5s, and to a lesser. There are a number of different card counting systems or 'counts' that can be used when counting cards at blackjack. This video will explain the different ty. The underlying principle behind card counting is that a deck rich in tens and aces is good for the player, a deck rich in small cards is good for the dealer. When the counter knows the odds are in his favor, he will bet more, and adjust his playing strategy to stand, double, and split in some plays where basic strategy says to stand. Card Counting Systems Ace-Five. If you’re interested in learning how to card count, but aren’t sure you want to learn a complex system right away, the Ace-Five Count might be right for you. It’s also perfect for casual players that want to cut into the house edge and have the possibility of ending up slightly ahead of the casino, but aren’t worried about playing blackjack for a living or squeezing out as big an advantage.

Find out how to count cards in blackjack and learn the difference between running and true counts in hi lo card couting strategy.

What is Card Counting?

Card counting is a system of keeping track of all the dealt cards in the game in order to ascertain when the deck favors the dealer and when the player has higher odds. The odds are determined by the number the counter keeps in his mind. This number is found by adding or subtracting a definite number to a starting count of zero as the cards are dealt on the table.

The player determines the odds in the game and can vary his bet, betting more when the deck has high player odds and betting less when the deck favors the house.

Values of Cards

To keep track of and count all the dealt cards in blackjack, all the cards in the deck have particular values which are different from the traditional values used for counting the hand total. Blackjack card counters use the following values of cards:

count as +1

Best Card Counting System

count as 0

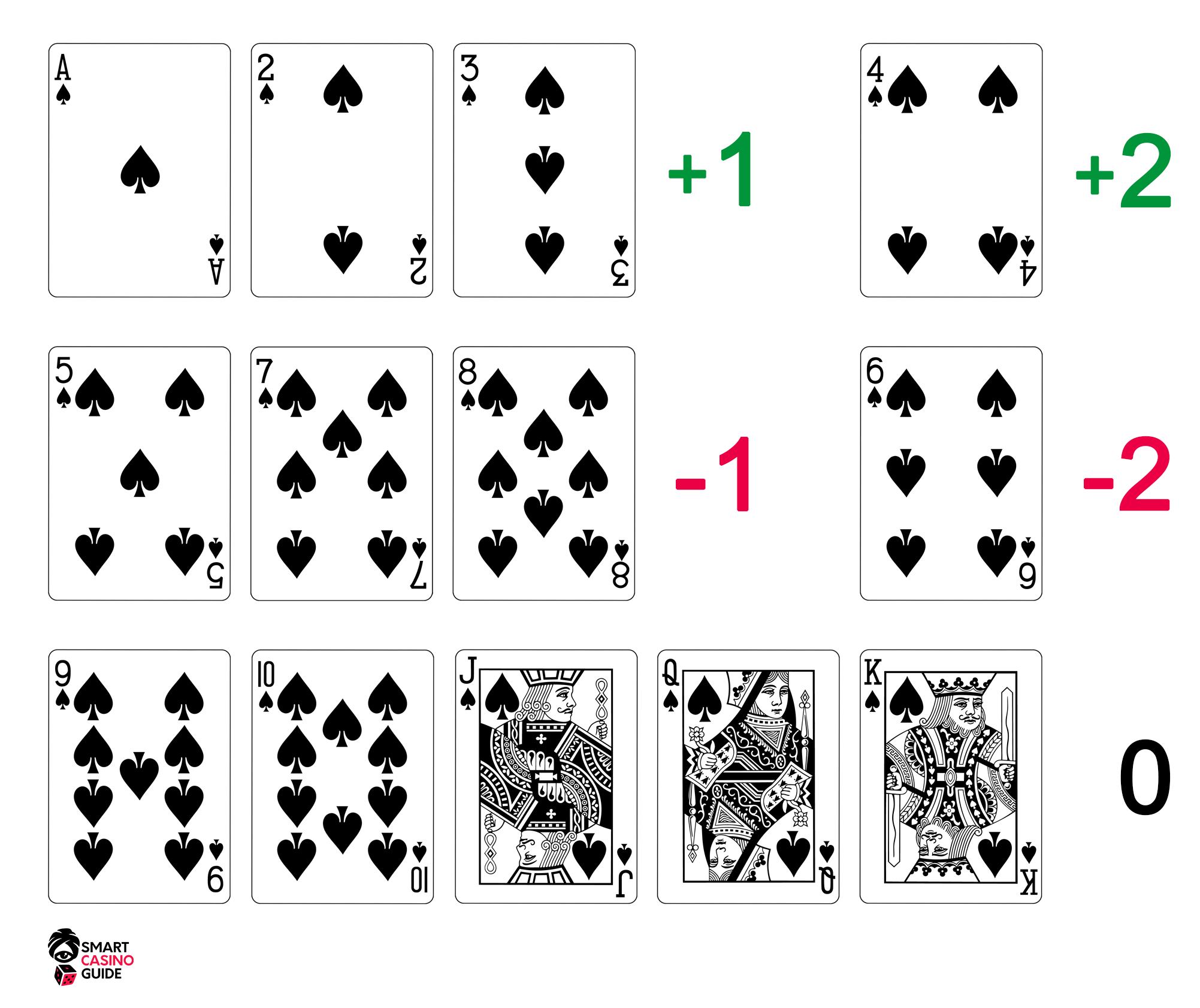
count as -1

Card Counting in Action

Let's consider an example of a real blackjack game and count the cards as they are dealt.

Above you can see two players at a blackjack table. The cards are dealt and the counter starts counting in his mind.

The first cards are:

If you look at the section Values of Cards above, you will see the value of each card. All you have to do is to add the values together.

1+0−1+0+0 = 0

The game continues and the players can choose from the available options.

The player on the first base stands and takes no more cards. The player on the second base, splits and gets a 9 and an Ace. The dealer reveals the hole card and has a total of 17. The new cards here are:

Now we add the value of these cards to the count total we had before.

0+0−1−1 = −2

The overall count for this game now is -2.

This count means that mostly high cards have been dealt and the deck is now full of small value cards, which favors the dealer. The counter will most probably decrease his bet and play the game with a smaller risk.

The game continues and the next hands are dealt. The counter now keeps on counting the cards proceeding from the number he had on the previous game (-2).

However, this Count can only be applied when the game is played with 1 deck of cards and is called a Running count. Due to the fact the running count can only be used for a game with one deck and the system is not accurate if used for more than 1 deck, this system is called an Unbalanced card-counting system.

Balanced vs. Unbalanced Count

Unbalanced card-counting system - is a system that uses the count of a cards one by one as they are dealt and is used in a 1-deck blackjack game.

Balanced card-counting system - is a system that applies the method of Unbalanced card counting and modifies it according to the number of decks used in the game. This method enables the counter to accurately calculate the correct result of card counting and apply it in the game.

The balanced count is usually viewed as an application of the Running count and thus the player can convert the result into the True count.

In order to convert the Running count into the True count, the counter should divide the result of the running count by the number of decks left in the game.

For example, if the running count is 12, and there are 4 decks in the shoe left, the player gets a true count of 3 (12/4=3)

Basics Of Card Counting

The True count is the basic system of card counting. This method helps you choose how much and when to bet. In addition it tells you when it is better to switch from the recommendations of basic strategy and either risk or surrender.

What do I do with the result of the count?

Remember that a positive count tells you it's time to bet more as there are high cards left in the deck. In general, when the true count is higher than 4 there are lots of high cards in the deck and you should increase the bet and be careful when you hit. However, this rule may vary for a different number of decks and no one is qualified enough as to tell you when to risk and when not to.

The most difficult part of this count is to predict how many decks are left in the shoe.

bet more'>

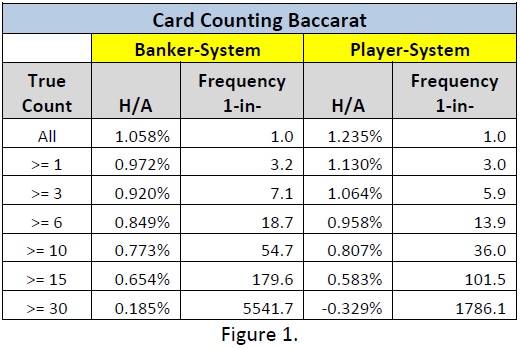
In order to find out more about the average results of the count and how often this or that outcome may occur, you can look at the tables with generated hands for games with One, Four, Six or Eight decks of cards.

Getting the Edge

Card counting is based on the fact that when the deck is full of high cards, it has a big advantage for the player and when the deck is full of small cards it is good for the dealer. When the deck favors you, you should make larger bets and make smaller ones when it is good for the dealer.

This is because the dealer has to continue to take cards when he has 16 whereas you can stop any time you wish and not risk going bust when the deck has lots of 10 cards. Likewise, the deck favours the dealer when is full of small cards as he is less likely to bust when he hits.

Needless to say card counting requires much practice, but the correct use of this technique may give you a 2% edge over the casino.

Advanced counting systems

Best books on Card Counting

• Standford Wong — Professional Blackjack (High/Low Strategy)
• Ken Uston — Million Dollar Blackjack (Plus/Minus Strategy)

Counting is the process of determining the number of elements of a finite set of objects. The traditional way of counting consists of continually increasing a (mental or spoken) counter by a unit for every element of the set, in some order, while marking (or displacing) those elements to avoid visiting the same element more than once, until no unmarked elements are left; if the counter was set to one after the first object, the value after visiting the final object gives the desired number of elements. The related term enumeration refers to uniquely identifying the elements of a finite (combinatorial) set or infinite set by assigning a number to each element.

Counting sometimes involves numbers other than one; for example, when counting money, counting out change, 'counting by twos' (2, 4, 6, 8, 10, 12, ...), or 'counting by fives' (5, 10, 15, 20, 25, ...).

There is archaeological evidence suggesting that humans have been counting for at least 50,000 years.^[1] Counting was primarily used by ancient cultures to keep track of social and economic data such as the number of group members, prey animals, property, or debts (that is, accountancy). Notched bones were also found in the Border Caves in South Africa that may suggest that the concept of counting was known to humans as far back as 44,000 BCE.^[2] The development of counting led to the development of mathematical notation, numeral systems, and writing.

Forms of counting[edit]

Counting can occur in a variety of forms.

Counting can be verbal; that is, speaking every number out loud (or mentally) to keep track of progress. This is often used to count objects that are present already, instead of counting a variety of things over time.

Counting can also be in the form of tally marks, making a mark for each number and then counting all of the marks when done tallying. This is useful when counting objects over time, such as the number of times something occurs during the course of a day. Tallying is base 1 counting; normal counting is done in base 10. Computers use base 2 counting (0s and 1s), also known as Boolean algebra.

Counting can also be in the form of finger counting, especially when counting small numbers. This is often used by children to facilitate counting and simple mathematical operations. Finger-counting uses unary notation (one finger = one unit), and is thus limited to counting 10 (unless you start in with your toes). Older finger counting used the four fingers and the three bones in each finger (phalanges) to count to the number twelve.^[3] Other hand-gesture systems are also in use, for example the Chinese system by which one can count to 10 using only gestures of one hand. By using finger binary (base 2 counting), it is possible to keep a finger count up to 1023 = 2¹⁰ − 1.

Various devices can also be used to facilitate counting, such as hand tally counters and abacuses.

Card Counting Systems For Blackjack

Inclusive counting[edit]

Different Card Counting Systems App

Inclusive counting is usually encountered when dealing with time in the Romance languages.^[4] In exclusive counting languages such as English, when counting '8' days from Sunday, Monday will be day 1, Tuesday day 2, and the following Monday will be the eighth day. When counting 'inclusively,' the Sunday (the start day) will be day 1 and therefore the following Sunday will be the eighth day. For example, the French phrase for 'fortnight' is quinzaine (15 [days]), and similar words are present in Greek (δεκαπενθήμερο, dekapenthímero), Spanish (quincena) and Portuguese (quinzena). In contrast, the English word 'fortnight' itself derives from 'a fourteen-night', as the archaic 'sennight' does from 'a seven-night'; the English words are not examples of inclusive counting.

Names based on inclusive counting appear in other calendars as well: in the Roman calendar the nones (meaning 'nine') is 8 days before the ides; and in the Christian calendar Quinquagesima (meaning 50) is 49 days before Easter Sunday.

Musical terminology also uses inclusive counting of intervals between notes of the standard scale: going up one note is a second interval, going up two notes is a third interval, etc., and going up seven notes is an octave.

Education and development[edit]

Simple Card Counting System

Learning to count is an important educational/developmental milestone in most cultures of the world. Learning to count is a child's very first step into mathematics, and constitutes the most fundamental idea of that discipline. However, some cultures in Amazonia and the Australian Outback do not count,^[5][6] and their languages do not have number words.

Many children at just 2 years of age have some skill in reciting the count list (that is, saying 'one, two, three, ...'). They can also answer questions of ordinality for small numbers, for example, 'What comes after three?'. They can even be skilled at pointing to each object in a set and reciting the words one after another. This leads many parents and educators to the conclusion that the child knows how to use counting to determine the size of a set.^[7] Research suggests that it takes about a year after learning these skills for a child to understand what they mean and why the procedures are performed.^[8][9] In the meantime, children learn how to name cardinalities that they can subitize.

Counting in mathematics[edit]

In mathematics, the essence of counting a set and finding a result n, is that it establishes a one-to-one correspondence (or bijection) of the set with the set of numbers {1, 2, ..., n}. A fundamental fact, which can be proved by mathematical induction, is that no bijection can exist between {1, 2, ..., n} and {1, 2, ..., m} unless n = m; this fact (together with the fact that two bijections can be composed to give another bijection) ensures that counting the same set in different ways can never result in different numbers (unless an error is made). This is the fundamental mathematical theorem that gives counting its purpose; however you count a (finite) set, the answer is the same. In a broader context, the theorem is an example of a theorem in the mathematical field of (finite) combinatorics—hence (finite) combinatorics is sometimes referred to as 'the mathematics of counting.'

Advanced Card Counting

Many sets that arise in mathematics do not allow a bijection to be established with {1, 2, ..., n} for anynatural numbern; these are called infinite sets, while those sets for which such a bijection does exist (for some n) are called finite sets. Infinite sets cannot be counted in the usual sense; for one thing, the mathematical theorems which underlie this usual sense for finite sets are false for infinite sets. Furthermore, different definitions of the concepts in terms of which these theorems are stated, while equivalent for finite sets, are inequivalent in the context of infinite sets.

Is Counting Cards Hard

The notion of counting may be extended to them in the sense of establishing (the existence of) a bijection with some well-understood set. For instance, if a set can be brought into bijection with the set of all natural numbers, then it is called 'countably infinite.' This kind of counting differs in a fundamental way from counting of finite sets, in that adding new elements to a set does not necessarily increase its size, because the possibility of a bijection with the original set is not excluded. For instance, the set of all integers (including negative numbers) can be brought into bijection with the set of natural numbers, and even seemingly much larger sets like that of all finite sequences of rational numbers are still (only) countably infinite. Nevertheless, there are sets, such as the set of real numbers, that can be shown to be 'too large' to admit a bijection with the natural numbers, and these sets are called 'uncountable.' Sets for which there exists a bijection between them are said to have the same cardinality, and in the most general sense counting a set can be taken to mean determining its cardinality. Beyond the cardinalities given by each of the natural numbers, there is an infinite hierarchy of infinite cardinalities, although only very few such cardinalities occur in ordinary mathematics (that is, outside set theory that explicitly studies possible cardinalities).

Counting, mostly of finite sets, has various applications in mathematics. One important principle is that if two sets X and Y have the same finite number of elements, and a function f: X → Y is known to be injective, then it is also surjective, and vice versa. A related fact is known as the pigeonhole principle, which states that if two sets X and Y have finite numbers of elements n and m with n > m, then any map f: X → Y is not injective (so there exist two distinct elements of X that f sends to the same element of Y); this follows from the former principle, since if f were injective, then so would its restriction to a strict subset S of X with m elements, which restriction would then be surjective, contradicting the fact that for x in X outside S, f(x) cannot be in the image of the restriction. Similar counting arguments can prove the existence of certain objects without explicitly providing an example. In the case of infinite sets this can even apply in situations where it is impossible to give an example.^{[citation needed]}

The domain of enumerative combinatorics deals with computing the number of elements of finite sets, without actually counting them; the latter usually being impossible because infinite families of finite sets are considered at once, such as the set of permutations of {1, 2, ..., n} for any natural number n.

See also[edit]

• Yan tan tethera (Counting sheep in Britain)

References[edit]

1. ^An Introduction to the History of Mathematics (6th Edition) by Howard Eves (1990) p.9
2. ^'Early Human Counting Tools'. Math Timeline. Retrieved 2018-04-26.
3. ^Macey, Samuel L. (1989). The Dynamics of Progress: Time, Method, and Measure. Atlanta, Georgia: University of Georgia Press. p. 92. ISBN978-0-8203-3796-8.
4. ^James Evans, The History and Practice of Ancient Astronomy. Oxford University Press, 1998. ISBN019987445X. Chapter 4, page 164.
5. ^Butterworth, B., Reeve, R., Reynolds, F., & Lloyd, D. (2008). Numerical thought with and without words: Evidence from indigenous Australian children. Proceedings of the National Academy of Sciences, 105(35), 13179–13184.
6. ^Gordon, P. (2004). Numerical cognition without words: Evidence from Amazonia. Science, 306, 496–499.
7. ^Fuson, K.C. (1988). Children's counting and concepts of number. New York: Springer–Verlag.
8. ^Le Corre, M., & Carey, S. (2007). One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition, 105, 395–438.
9. ^Le Corre, M., Van de Walle, G., Brannon, E. M., Carey, S. (2006). Re-visiting the competence/performance debate in the acquisition of the counting principles. Cognitive Psychology, 52(2), 130–169.